Gold I Greedy Compilation List

각 칸을 land와 water라고 부르자. 왼쪽의 어느 land과 오른쪽의 어느 land 하나를 잡아 이 둘을 잇는 경로를 생각하자. 이것이 최적해라고 하자. 만약 경로 중간에 새로운 land를 거치는 경우, 시작점이나 끝점 중 하나를 그 land로 바꾸면 더 짧은 경로가 나오므로, 최적해는 시작점과 끝점을 제외하면 모두 river를 지나는 경로이다. 또한 왼쪽 land의 좌표를 $(x_1, y_1)$이라 하고, 오른쪽을 $(x_2, y_2)$라고 하면, 두 지점을 잇는 최단경로로 다리를 메우는 것이 최적이다. 이 때 필요한 bridge의 개수는 $|x_1-x_2|+|y_1-y_2|-1$개이다.

문제의 조건 상, river의 left boundary 전체가 right boundary보다 왼쪽이므로, 항상 $x_1 \leq x_2$이며, 또한 $x_1$은 $y=y_1$ row의 river 바로 왼쪽 land, $x_2$는 $y=y_2$ row의 river 바로 오른쪽 land일 때 최적임을 알 수 있다. 따라서 $y_1 \leq y_2$인 case와 $y_1 > y_2$인 case를 분리해서 각각 계산해주면 되며, 이는 입력을 한 줄씩 받으면서 left boundary 칸들의 $x+y$ 최댓값, right boundary 칸들의 $y-x$ 최댓값을 관리해나가면 된다. 즉 $i$번째 row를 처리할 때 $1$번째부터 $i-1$번째 row의 값과 계산을 합치는 것이다.

공식 정답 코드가 있어서, 코드를 보고 내가 해석한 결과를 적는다. 다른 해석이 있다면 모르겠는데, 개인적으로는 하늘에서 뚝 떨어진 motivation처럼 느껴진다.

WLOG $x_1 \leq x_2 \leq \ldots \leq x_n$라고 하자. 웜홀의 양 끝 점이 $a \leq b$라고 하자. $k$를 $x_k \leq \frac{x_1+x_n}{2}$인 최댓값으로 정의하자. 이 때, 이 문제의 답은 $\max(x_k-x_1, x_n-x_{k+1})$임을 증명할 것이다. WLOG $x_k-x_1 \geq x_n-x_{k+1}$라고 가정한다.

• 이 답을 가지는 웜홀 배치가 존재함을 먼저 보인다. $a = \frac{x_1+x_k}{2}$, $b = \frac{x_{k+1}+x_n}{2}$로 두면 된다. 그러면 $x_1 \Leftrightarrow x_k$의 이동이 최대 거리를 가지는 이동이 됨을 쉽게 보일 수 있다.

• 또한 이 값보다 최대 거리가 작아질 수 있는 웜홀 배치가 없음을 보이자. $a \geq \frac{x_1+x_n}{2}$이거나 $b \leq \frac{x_1+x_n}{2}$인 경우 반드시 이동 거리가 $\frac{x_1+x_n}{2} > x_k-x_1$ 이상이 되는 점 pair가 생기므로 불가능하다. 따라서 $a \leq \frac{x_1+x_n}{2} \leq b$이고, $x_1 \Leftrightarrow x_k$의 이동 거리가 짧아져야 하므로, 이들은 반드시 웜홀을 통한 이동으로 이득을 보아야 한다. 즉 $x_k-a \geq b-x_k$도 성립. 그러나 이 경우 $x_k \Leftrightarrow x_n$ 이동이 웜홀로 볼 수 있는 이동 거리의 이득이 사라지므로, $x_n-x_k \geq \frac{x_1+x_n}{2}$여서 모순.

WLOG $x$ 기준으로 점들이 정렬되어있음을 가정한다. 부분그래프 $C$가 고른 index들이 $i_1 < i_2 < \ldots < i_{|C|}$라고 하자. 핵심적인 관찰은 $w_{i_k} + w_{i_{k+1}} \leq x_{i_{k+1}}-x_{i_k}$가 $1 \leq k < |C|$에 대해서 성립하기만 하면 임의의 두 점이 연결될 조건이 만족된다는 것이다. 그러므로 순서대로 점들을 읽어나갈 때 가장 마지막으로 $C$에 포함시키기로 한 점만 확인하면 되므로, dp를 적용할 수 있다. 마지막으로 $C$에 포함된 점이 $j$이고 현재 보는 점이 $i > j$일 때 연결 조건은 $x_j+w_j \leq x_i-w_i$이므로, LIS 문제와 비슷하게 접근이 가능하다.

dp[i]를 $i$를 마지막으로 포함하는 부분그래프의 최대 크기로 정의하고, lb[i]를 $dp[j]=i$인 $1 \leq j \leq i$ 중 $x_j+w_j$의 최솟값으로 정의하자. LIS를 풀 때처럼 $i$번째 점을 처리할 때 $x_i-w_i$에 대한 upper_bound 위치의 값과 $x_i+w_i$ 중 더 작은 값으로 갱신하는 작업을 반복하면 $lb$의 monotonicity가 항상 유지된다. 왜냐하면 $x_j+w_j \leq x_i-w_i < x_i+w_i$가 성립하기 때문.

지문에는 명시되어 있지 않으나, 복원한 그래프에 multiedge가 있으면 WA로 처리된다고 한다. 다만 이러한 점을 제외하더라도, 복원 가능하다면 multiedge가 없는 그래프로도 복원이 가능함으로 이러한 경우만 고려하자.

먼저 자명한 경우부터 고려한다. 최단거리는 metric이므로, metric의 조건이 만족되지 않는 input은 미리 복원 불가능 판정을 내려둬야 한다. 입력으로 주어지는 $i$와 $j$ 사이의 최단거리를 $d_{ij}$라고 쓰자. 여기서 가능한 모든 조합 $1 \leq i, j, k \leq n$에 대해 $d_{ij} > d_{ik} + d_{kj}$인 경우가 존재하면 항상 복원 불가능이다.

이제는 위의 조건을 만족하는 입력만 고려할 수 있다. 이 경우, $1 \leq i < j \leq n$인 모든 정점 쌍에 대해 $i$와 $j$ 사이에 $d_{ij}$ 길이의 간선이 있는 그래프는 항상 조건을 만족한다. 이 그래프의 간선 집합을 $E$라고 하자. 그러나 이 경우 $|E| = \binom{n}{2}$로 비효율적이다. 따라서 조건을 만족하는 그래프 중 간선 개수가 최소인 그래프를 떠올리는 것이 motivation이 될 수 있겠다. 이 때의 간선 집합을 $E_{opt}$라고 정의하자.

또한 다음 알고리즘에 따라 얻어지는 $E$의 subset $E'$을 생각하자.

Sort E by non-decreasing weight
E' = {}
for (u, v) in E:
    if d_uv > (distance between u and v in E'):
        add (u, v) to E
return E'

목표는 $|E'| = |E_{opt}|$임을 보이는 것이다. 귀류법으로 $|E'| > |E_{opt}|$라고 하자. 그러면 $(E' \setminus E_{opt}) \neq \emptyset$이고, 이 중 weight이 최소인 간선을 $(u, v)$라 하자. $E_{opt}$에 의해서도 $u$와 $v$ 사이의 최단거리가 $d_{uv}$여야 하므로, 어떤 정점 $w \neq u, v$가 존재하여 $d_{uw}+d_{wv} = d_{uv}$를 만족한다. 간선의 weight이 항상 양수이므로, 위 알고리즘은 $(u, w)$와 $(w, v)$를 $(u, v)$보다 먼저 처리했을 것이고, 따라서 $(u, v)$가 처리되는 시점에는 이미 $u \Leftrightarrow w$를 $d_{uw}$의 거리로, $w \Leftrightarrow v$를 $d_{wv}$의 거리로 이동하는 방법이 모두 존재했다는 뜻이다. 즉 if 조건이 실행될 수 없으므로, $(u, v) \in E'$임에 모순.

그러므로 위의 알고리즘으로 만들어진 $|E'|$이 곧 문제의 답이기도 하다.

Undirected weighted graph $G$가 주어졌을 때, subgraph $H$ 위에서의 거리가 $G$ 위에서의 거리를 $t$-approximate할 때 $H$를 $G$의 $t$-spanner라고 부른다. 그러므로 $H$의 edge size를 최대한 줄일 수 있다면, 이는 곧 그래프 위의 metric을 효율적으로 표현할 수 있다는 뜻이다. $k \geq 2$인 integer $k$에 대해, $O(n^{1+1/k})$의 edge size를 갖는 $(2k-1)$-spanner가 존재함이 알려져 있고, 이것이 Erdos girth conjecture가 성립할 때 optimal임도 알려져 있다. 이 논문이 그러한 $t$-spanner를 찾는 방법을 알려주는데, 실제로 $E'$을 구하는 위의 코드는 이 논문에서 제시된 $t=1$일 때의 $t$-spanner를 구하는 방법이기도 하다. Optimality에 관해서는 이거를 참조해봐도 좋겠다.

Trivia의 graph spanner에 대한 글이 @koosaga님의 블로그에 올라온 걸 발견했다. Spanner를 더 효율적으로 계산하는 방법에 대해 서술되어 있다. 이 글을 참조해도 좋을 듯.

문제의 notation을 따라, 어떤 쿼리의 각을 $(a, b)$로 두자. 이 때 최적해의 후보가 될 수 있는 도로는 $b$의 바로 오른쪽 혹은 바로 왼쪽 도로 2개뿐임을 보이면 된다. 즘명은 매우 간단한데, 내가 바깥쪽 반지름 $r_2$에서 이동하는 각을 $\theta$만큼 아낄 수 있다면 안쪽 반지름 $r_1 < r_2$에서 이동할 각은 길어져야 $\theta$뿐이기 때문이다.

문제를 처음 봤을 때 접근할 만한 방식으로 증명을 써 보겠다. $S(x)$를 $x \geq 0$에 대해 $x$의 $10$진법 표현의 자릿수 합으로 정의하자. 또한 $|x|$를 10진법 표현에서의 자릿수라고 하자.

먼저 입력이 양이 아닌 정수 $-n$ $(n \geq 0)$이라고 하자. 이 경우 문제를 다시 쓰면 $n < m$이고 $S(m) = S(n)+1$인 최소의 $m$을 찾는 문제가 된다. $n = \overline{ab99\dots9}$ ($b$는 $9$가 아닌 단일 자릿수를 의미) 그러면 $m = \overline{a(b+1)99\dots9}$가 답이 되는데, 증명은... 이게 충분한 설명일지는 모르겠으나, 가능한 답의 후보를 순서대로 $n+1$, $n+2$, $\dots$처럼 생각했을 때 이 $m$값이 이전에 나오는 수들은 자릿수의 합이 $S(n)+1$일리가 없기 때문이다. 여기서 사용한 notation은 모든 자릿수가 $9$일 때 약간 애매해지는데, $b=0$으로 두고 생각하면 된다. 즉 입력이 $-99$라면 답은 $-199$라는 의미.

이제 입력이 양의 정수일 때가 핵심이다. 먼저 답이 음수가 되지 않는 입력만을 생각해보자. 입력 $n$과 답 $m$에 대해 $0 < m < n$이므로, 이들은 항상 $n = \overline{abc}$, $m = \overline{ab'c'}$과 같이 표현된다. $b$와 $b'$은 단일 자릿수이고 $b'<b$를 만족하며, 편의 상 $|n|=|m|$이되 $m$은 leading zero를 가질 수도 있다고 하자. 만약 $0 \leq b' \leq b-2$인 $m$이 조건을 만족한다면, $b' = b-1$로 두고 $c'$에서 적절히 $0$이 아닌 자릿수들을 감소시키는 작업이 항상 가능하므로 ($S(c') \geq S(c)+2 \geq 0$이기 때문), 최대인 $m$은 항상 $b' = b-1$을 만족한다.

그러므로 $m > 0$이라면 $S(c') = S(c)+2$인데, 따라서 $S(c) \leq 9|c|-2$여야 한다. 우리는 $b$의 위치를 최대한 뒤쪽(least sig)으로 가져가기를 원하므로, $n$을 least significant digit부터 읽어가면서 $S(c) \geq 9|c|-2$가 되는 최소의 $|c|$를 알아냈다고 하자 (존재한다고 치자). 이제 $|c|+1$번째 least significant digit부터 볼 때 $0$이 아닌 최초의 자릿수가 $b$가 될 수 있는 최적의 위치이고, $m = \overline{ab'c'}$에서 $b'=b-1$의 위치와 자릿수까지 결정되었다면 $|c'|$개의 남은 자릿수에 $S(c')=S(c)+2$ 조건을 만족시키는 것은 greedy하게 큰 자릿수를 $9$로 먼저 채워나가는 방식으로 해결 가능.

이 방법의 예외는 다음 두 가지이다: $n = 799$여서 최소의 $|c| = |n|$인 경우나, 아니면 $n = 989$ 같은 수여서 $S(c) \leq 9|c|-2$인 $|c|$가 존재하지 않는 경우이다. 이 경우는 맨 처음에 했던 가정, $m > 0$이라는 조건이 깨지는 경우이다. 그러므로 답이 $-m$ $(m \geq 0)$이라고 두면, 이제는 $n$과 $m$의 대소 관계 없이 $S(m) = S(n)+1$인 최소의 $m$을 찾는 문제가 된다. 이건 방금 전에 $c'$을 구성하는 greedy와 상황이 완전히 똑같으므로, 증명 끝.

기본적인 전략은 배열 $A$를 incremental하게 만들어나가는 것이다. 그러므로 증명은 induction의 형태와 비슷하다. median 조건 $B_1, B_2, \cdots, B_{i-1}$을 모두 만족하도록 길이 $2i-3$ 배열 $A$가 만들어져 있다고 하자. 즉 여기서 증명하고 싶은 것은, $i$번째 median 조건 $B_i$까지도 만족하게 $A$에 $2$개의 수를 더 추가할 수 있다는 것이다.

그 전에 $i \leq B_i \leq 2n-i$가 항상 만족됨을 짚고 넘어가자. 이것이 성립하지 않으면 조건을 만족하는 순열 $A$가 존재하지 않으므로, 이 문제에서 들어오는 입력은 항상 이 조건을 만족한다.

• $B_i = B_{i-1}$이라고 하자. 이 경우 $B_i$보다 작은 원소 하나와 큰 원소 하나를 $A$에 추가할 수 있으면 된다. 여기서 확인해야 할 조건은 $A$가 순열이므로, 이미 $A$에 들어간 원소를 다시 집어넣을 수 없다는 것이다. 만약 $1, 2, \cdots, B_{i-1} = B_i$이 이미 $A$에 모두 들어가 있어서 $B_i$보다 작은 원소를 추가할 수 없었다고 하자. 그러나 이는 현재 순열의 상태 $A$가 $i-1$번째 median 조건 $B_{i-1}$을 만족하고 있다는 사실에 모순이다. $A$의 크기 순 $i-2$번째 원소가 $B_{i-1}$이어야 하는데, $i \leq B_i = B_{i-1}$이므로 $A$의 크기 순 $i-2$번째 원소가 $i-2$이기 때문이다.

다만 여기서 $A$에 넣는 원소에 추가적인 조건을 걸어줘야 한다. 지금처럼 $B_i$보다 작은 원소를 넣어야 하면, 지금까지 $A$에 포함되지 않은 수 중 가장 작은 수를 넣어줘야 하고, 반대의 상황에서는 가장 큰 수를 넣어줘야 한다. 이 성질은 아래에서 쓰인다.

• $B_i < B_{i-1}$이라고 하자. 이번에는 두 가지 경우가 있다. 첫 번째는 $B_j = B_i$인 $j < i$가 존재하는 경우이다. 이 경우 $A$에 $B_i$보다 작은 원소를 $2$개 넣어야 일단 median이 작아지는 것을 기대할 수 있으므로, 입력으로 들어오는 $B_1, \cdots, B_i$에서 $B_{i-1}$와 $B_i$는 크기 순으로 인접한 원소임이 보장된다. 따라서 $A$에 $B_i$보다 작은 원소를 $2$개 넣을 수 있는지, 지금까지 $A$에 $B_i < x < B_{i-1}$인 $x$를 넣은 적이 없는지를 증명해야 한다.

첫 번째 이슈는 위에서와 같은 방법으로 증명할 수 있다. $i \leq B_i < B_{i-1}$이므로, $A$에는 $i+1$보다 작은 원소가 많아야 $i-2$개 존재하며, 따라서 $[1, i] \subseteq [1, B_i]$ 구간에서 아직 사용하지 않은 원소가 최소 $2$개 존재한다. 두 번째 이슈는 좀 더 tricky하다. $B_i < x < B_{i-1}$인 $x$가 그보다 작은 원소를 다 사용해서 $A$에 어쩔 수 없이 포함되었다는 건 첫 번째 이슈를 해결한 방법과 마찬가지로 불가능하다. 또한 $x$보다 큰 원소를 다 사용해서 $A$에 포함되었음도 비슷한 이유로 불가능하다. 이는 $B_{i-1}$이 median이어야 하는 시점에 $[x, 2n-1]$이 전부 $A$에 이미 포함되었다는 뜻이므로, $i-1$번째 median이 $B_{i-1}$보다 컸어야 했을 것이기 때문이다.

• $B_i < B_{i-1}$이고, $B_i$는 이전의 median 조건에서 사용된 수가 아니었다고 하자. 그러나 $B_i \in A$였다고 하면, $[1, B_i] \subset A$여야 하는데, $i \leq B_i$이므로 $A$의 $i-1$번째 수가 $i-1$인 것이 확정이므로 $B_i < B_{i-1}$에 모순. 따라서 $B_i \not\in A$였을 것이므로, 우선 $A$에 $B_i$를 추가해야 한다. 그러면 남은 작업은 $B_i$ 미만의 수를 하나 더 $A$에 넣을 수 있는지, $A$에 $B_i < x < B_{i-1}$인 $x$가 존재하지 않음을 확인하는 것이다. 조건 상 $i+1 \leq B_{i-1}$이고, $A$에 $B_{i-1}$보다 작은 수가 정확히 $i-2$개이므로 $B_i$ 미만의 수도 최소 하나 존재함은 자명. 또한, 만약 그러한 $x \in A$가 존재한다면 이는 $B_j = x$인 어떤 $j < i$에서 유래하지 않았음이 보장된다. 왜냐하면 median이 최대 $1$개만 이동한다는 점에서, $B_{i-1}$ 다음 median이 $B_i$인 것에 모순되어 입력 조건을 만족하는 수열이 없게 되기 때문이다. 그러므로 $B_i \not\in A$였다는 사실까지 생각하면, $x$는 어떤 순간 $[x+1, 2n-1]$ 범위의 수들이 전부 $A$에 들어간 상황 이후에 어쩔 수 없이 $A$에 추가되었다는 의미가 된다. 그러나 이는 이전 케이스와 같은 이유로 현재 $B_{i-1}$이 $A$의 median이라는 사실에 모순.
• $B_i > B_{i-1}$인 상황은 위와 정확히 대칭적이다. 생략.

다른 그리디 문제치고는 쉬운 편이니 짧게 쓴다. 임의의 양의 정수 $y$는 $y = \sum_{i=0}^{\infty} y_i \cdot 36^i$과 같은 유일한 $36$진법 표현을 갖는다. 따라서, 입력으로 주어지는 수를 $x_1, \cdots, x_n$으로 쓰면, 이들의 합은 다음과 같다. $$ \sum_{i=1}^{n} \sum_{j=0}^{49} x_{ij} \cdot 36^j $$ 어떤 $0 \leq c < 36$에 대해 $x_{ij} = c$인 것들만 모아쓰면, $x_{ij} = c$인 $(i, j)$ pair 개수를 $M_c$라고 할 때, 위의 식은 다음과 같이 변형된다. $$ \sum_{c=0}^{35} \sum_{i=1}^{M_c} c \cdot 36^{k_i} $$ 그러므로 특정한 $c$를 'Z', 즉 $35$로 바꾸는 시행은 전체 수들의 합을 $(35-c) \cdot \sum_{i=1}^{M_c} 36^{k_i}$만큼 증가시키며, 이 값들은 $c$끼리 서로 독립이므로, 이 값이 가장 큰 $k$개의 자릿수를 'Z'로 바꿔주면 된다.

우선 구슬은 $2$개씩만 없앨 수 있으므로, 전체 구슬의 개수가 홀수이면 아무리 잘해도 어떤 구슬 $1$개는 못 없앤다. 각 구슬이 $x_1 \geq x_2 \geq \cdots \geq x_n$개 있고, 전체 구슬 개수가 $s = \sum_{i=1}^{n} x_i$라고 하자. 우선 $x_1 \gg s-x_1$인 경우를 생각하자. 이 경우 $1$번이 아닌 모든 구슬을 $1$번과 대응시켜 없애도 $1$번 구슬이 많이 남을 텐데, 따라서 최종적으로 $1$번 구슬을 $2x_1-s$개보다 더 적게 남길 수는 없고, 실제로 그러한 결과를 만드는 충돌 방법이 존재하므로, $2x_1-s \geq 0$인 입력의 경우에는 이것이 바로 답이다.

남은 경우는 $2x_1 < s$인 경우인데, 결론부터 말하자면 $s$가 홀수이면 $1$개만 남길 수 있고, 짝수이면 전부 없앨 수 있다. 직관적으로 만들 수 있는 전략은, 항상 가장 많이 남은 구슬 두 종류씩을 하나씩 없애는 과정을 반복하는 것이다. 증명은 $s$에 대한 (강한) 귀납법으로 진행할 수 있다. 이 과정을 한 번 시행하면 남은 구슬은 $(x_1-1, x_2-1, x_3, \cdots, x_n)$이 된다. 여전히 $x_1-1 \geq x_3$인 경우 바뀐 상태는 $2(x_1-1) < s-2$를 만족한다. $x_1-1 < x_3$인 경우 $x_1 = x_3$였다는 의미이니, $x_1 = x_2 = \cdots = x_k > x_{k+1}$인 $k \geq 3$를 생각하자. 여기서 $(1, 2), (3, 4), \cdots$를 서로 충돌시켜 없애되, $k$가 홀수면 $(k-1, k)$를 한 번 더 충돌시키자. ($x_k = 1$인 경우는 따로 처리) $k$가 짝수이면 전체 합은 $k$가 감소했고, 최댓값은 $1$이 감소했으므로, 초기에 $kx_1 \leq s$였으므로 여전히 $s-k \geq k(x_1-1) > 2(x_1-1)$이 성립. $k$가 홀수이면 전체 합은 $k+1$이 감소했으므로, $s-k-1 \geq k(x_1-1)-1 \geq 2(x_1-1)$이 여전히 성립. Base case인 $s = 1$나 $x_1 = 1$인 경우들을 엮어주면 증명이 끝난다.

이 문제는 자주 나오는 형태이니, 풀이와 증명을 통째로 외우고 있어도 ps에서 나름 도움될 일이 있다고 생각한다. (이 증명은 재미없다고 생각하긴 하지만) 이 문제와 철학을 공유하는 문제들만 해도 꽤 많다. 예를 들어, 이거, 이거, 이거. 일반화된 버전도 존재한다.

사실 official solution이 뭔지 너무 대충 적혀 있어서, 아마 동치일 것으로 생각되는 전략으로 복원했다. 증명의 아이디어를 제공해준 @karuna에게 감사. 여담으로 @IBory님도 같은 아이디어를 제시하신 것으로 보아... 그냥 나만 어렵게 느낀 증명인 것 같다.

먼저 notation은 다음과 같다. 시작점이 $(0, 0)$, 끝점이 $(w-1, h-1)$이 되도록 좌표계를 설정한다. $P$를 수거할 parcel이 존재하는 위치들의 집합이라고 하자. 두 위치 $(x_1, y_1)$, $(x_2, y_2)$에 대해, $x_1 < x_2$이고 $y_1 > y_2$이면 $(x_2, y_2)$가 더 작다고 하자. 이 대소 관계는 decreasing sequence를 정의하기 위한 것이다. 엄밀하진 않으나, 한 수거원이 이동하는 경로는 increasing path라고 불러도 괜찮을 것임을 확인할 수 있다. (대소 관계가 정의되어 있다는 뜻은 아니다. $2$차원에 도식했을 때 그렇게 생겼다는 것이다. Decreasing이라는 네이밍의 기원은 맞다)

Greedy 전략은 다음과 같다. 어떤 수거원이 현재 위치하는 곳에서부터, 도달 가능한 $P$의 원소 중 $y$좌표가 가장 작은 위치를 $y = y_0$라고 하자. 현재 위치에서 $x$좌표를 바꾸지 않고 곧바로 $y = y_0$로 이동하고, 이후 $P$의 $y = y_0$인 지점 중 $x$좌표가 최대인 지점까지 이동한다. 여태껏 parcel을 수거한 위치를 $P$에서 제거하고, 이 과정을 수거원이 끝점에 도달할 때까지 반복한다. 일련의 과정을 모든 parcel을 수거할 때까지 새로운 수거원에 대해 반복한다.

초기 $P$에서 찾을 수 있는 longest decreasing sequence (이하 LDS)의 길이가 $L$이라고 하자. 이제 위의 greedy 전략은 수거원이 한 명 작업을 마칠 때마다 $P$의 LDS 길이를 정확히 $1$만큼 감소시킴을 보일 것이다. 또한 $L$명 미만의 수거원으로는 $P$의 모든 parcel을 수거할 수 없음을 보인다. $P$의 각 원소 $a$마다, $a$로 끝나는 decreasing sequence의 최대 길이를 $L_a$라고 정의하자. 이 때 이 수거원은 $L_a = L$인 모든 $a \in P$ 위치를 지나게 됨을 보이면 충분하다. 그러한 위치들 중 $y$좌표가 최소인 위치 (같다면 $x$좌표가 더 큰 곳)을 $(X, Y)$라고 하자.

수거원이 $(X, Y)$를 지나지 않는다고 가정하면, 수거원은 $y = Y$ line을 $x < X$ 위치에서 넘거나 $x = X$ line을 $y < Y$ 위치에서 넘어야 한다. Greedy 전략에 따르면, 수직 방향 이동은 $P$의 어떤 지점을 방문하고 (혹은 시작점) 그 다음으로 도달 가능한 위치 중 $y$가 최소인 지점을 향하는 것이므로, $y = Y$에 위치하는 $(X, Y)$ 지점을 무시하고 $y = Y$ line을 넘을 리가 없다. 이전에 위치하던 점이 $x > X$이고 $y < Y$인 위치였다면 LDS의 길이가 $L+1$이 되어 모순이다. 또한 수평 방향 이동은 $P$의 아직 방문하지 않은 위치를 향한 이동뿐이므로, 이 경우도 불가능. 그리고 $L_a = L$인 $a$ 위치들은 서로 대소 관계가 성립하지 않는 위치에 놓여 있고, 따라서 바로 위에서 증명한 성질에 따라 $(X, Y)$에 도달하면, 여전히 $L_a = L$인 위치들 전부가 여전히 도달 가능한 상태이다. 반복적으로 적용하면 결국 모든 위치를 다 지나게 됨을 알 수 있다.

마지막으로 최소 $L$명이 필요하다는 걸 증명하는 것인데, LDS를 아무거나 하나 잡으면, 임의의 수거원이 그들 중 $2$곳 이상을 동시에 지날 수 없으므로, $L-1$명 이하로는 못 지나는 parcel이 있다는 사실로부터 쉽게 유도된다.

사실상 같은 또다른 문제, Constructive Proof for Dilworth's Theorem.

id는 좌표압축되어있다고 치자. $x_1, x_2, \cdots, x_n$이 각 프로세스의 초기 priority라고 하자. $a \neq b$가 각각 시각 $t$와 $t+1$에 선택된 두 프로세스라고 하자. 먼저 시각 $t$가 되기 직전에 여태까지 $a$의 priority가 오른 횟수를 $i_a$, $b$에 대해서도 $i_b$라고 하자. $a < b$라고 하자. 이 경우 $a$가 시각 $t$에 $b$보다 먼저 선택되었으려면 $x_a+i_a \geq x_b+i_b$였다는 뜻이다. 또한 다르게 표현하자면 시각 $t+1$에는 $b$가 $a$보다 먼저 선택되었다는 뜻이고, 시각 $t$를 지나면서 $b$의 priority가 $1$ 증가했어야 하므로 $x_b+i_b+1 \geq x_a+i_a+1$이다. (id의 대소 관계가 바뀌었음을 유의) 따라서 $x_a + i_a = x_b + i_b$이다. 또한 $a > b$이면 같은 방식으로 부등식이 $2$개 세워지는데, 정확히 반대 방향이어서 $x_a+i_a = x_b+i_b+1$이 성립한다.

그러므로 이러한 필요조건들이 임의의 서로 다른 인접한 프로세스들 간에 형성되므로, $x_1 = 0$로 임의적으로 priority를 하나 정하면 $x_2, \cdots, x_n$도 전부 정해진다. (Scheduler가 선택한 적이 없는 id는 애초에 존재한 적이 없는 프로세스라고 생각해도 무방하므로, 입력에 $1$부터 $n$이 최소 한 번씩 나왔다고 하자) 여기서, 입력 조건 상 항상 답이 있는 경우만 주어진다고 보장되므로, 필요조건만 구했으나 이 지점에서 바로 $x$를 priority로 간주하면 된다. 각 프로세스의 실행을 마치는 데 필요한 시간은, 입력에서 그 프로세스가 등장한 횟수로 고정해도 된다. 왜냐하면 입력에서 어떤 프로세스 $j$가 마지막으로 나오는 지점 이후에는 $x_j$와 관련된 어떤 update도 일어나지 않으므로, 결과에 영향을 주지 않기 때문이다.

제대로 생각은 안 해봤는데, 위의 논증은 사실 더 강한 문제를 풀 수 있다고 생각된다. $x$끼리 consistent하게 방정식이 얻어지지 않으면 입력을 만족하는 output이 없다고 주장하는 것도 가능할 것 같다.

Official solution을 보면 비슷하지만 좀 더 constructive view에서 문제를 푸는데, 입력 수열을 순증가하는 수열로 쪼개서 보는 것이다. 이 관점에서 입력 조건이 consistent한지 판별하는 것은, 프로세스가 등장하는 수열 위치가 전부 연속적이어야 한다와 동치인 것 같다.

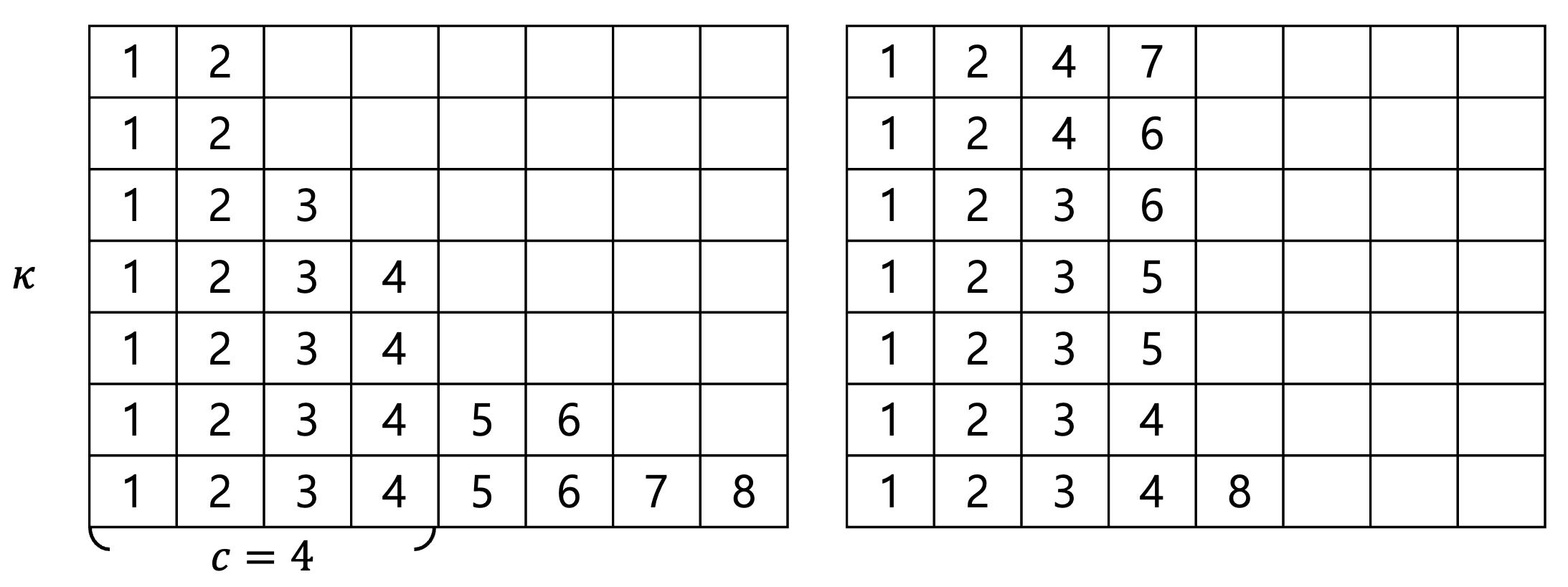
답에 대한 이분 탐색이 가능한 형태이다. 어떤 값 $\theta$가 답으로 가능한지 확인한다고 해 보자. 결정 문제로 바꾼 이후에는 $S'_i = \min(S_i, \theta)$로 둬도 답 여부가 바뀌지 않는다. 그렇게 만들어진 값을 $S'_1, S'_2, \cdots, S'p$라고 하자. 답이 yes이려면 먼저 최소한 $\sum{i=1}^{p} S'_i \geq \theta c$여야 한다. 흥미롭게도 이게 충분조건이기도 한데, 이건 예시 하나를 가져오는 게 더 설명이 빠를 것 같다. 아래 그림들은 $\theta = 7$, $c = 4$, $S' = [7, 7, 5, 4, 2, 2, 1, 1]$인 경우이며, 첫 번째 그림과 같이 입력 상태를 표현할 때, 두 번째 그림처럼 숫자를 잘 옮겨 쓰면 서로 다른 $c$개의 문제 조합을 풀어낸 $\theta$명의 사람들을 구성해낼 수 있다는 뜻이다.

(Undirected) Graph의 degree sequence가 주어져 있을 때, 조건을 만족하는 graph가 존재하는지 (no loop, no multiedge), 존재한다면 그 그래프를 하나 찾을 수 있는지는 매우 elementary하게 생겼고... (난이도가 어렵냐의 문제가 아니라) 실제로도 well-known이다. 그 조건과 관련된 것은 Erdős–Gallai theorem로 알려져 있으며, 찾는 알고리즘은 Havel-Hakimi algorithm으로 알려져 있는 듯하다. 세부 설명은... 인터넷에 널려 있을 다른 자료들로 대체하고, 증명의 개요(와 직관적 해설)만 적어둔다.

주어진 degree sequence를 $d_1 \geq d_2 \geq \cdots \geq d_n$이라고 하자. $\sum_{i=1}^n d_i$가 짝수인 것은 handshaking lemma의 결과이고, 사소하므로 스킵. 어떤 $k$개의 정점들을 고르자. 이들과 인접한 간선은 1) 선택된 정점들 사이의 간선과 2) 그들과 선택되지 않은 정점들 사이의 간선, 두 가지 종류가 있다. 이 정리가 말해주는 것은, 각 타입의 간선의 최댓값을 적당히 bound할 수 있으면, 선택된 정점 $k$개의 degree의 sum에도 그 bound가 적용된다는 것이다. 첫 번째 간선은 아무리 많아봤자 $\frac{k(k-1)}{2}$개임을 알 수 있다. 두 번째 간선은 선택하지 않은 정점들의 차수 합으로 bound된다. 따라서 $k$개의 선택을 차수가 가장 큰 정점 $k$개와 같은 극단적인 값으로 잡으면, 가장 강한 필요조건을 얻을 수 있다. Erdős–Gallai theorem은 이것이 결국 필요충분조건이라는 것을 말해준다.

실제로 존재하는지 찾는 알고리즘이 greedy 속성을 가진다. 핵심은 $(d_1, d_2, \cdots, d_n)$이 valid한 degree sequence이면, $(d_2-1, d_3-1, \cdots, d_{d_1+1}-1, d_{d_1+2}, \cdots, d_n)$도 valid하다는 것이다. (반대 방향도 당연히 성립) 그러므로 차수가 가장 큰 정점의 모든 인접 정점을, 그 다음으로 차수가 가장 많은 정점들과 매칭시켜주면 된다는 것이다. 증명의 핵심은 exchange argument로, $A-B$, $C-D$가 연결되어 있을 때 $A-C$, $B-D$로 바꿔도 degree sequence가 바뀌는 것은 아님을 이용한다.

처음 이 문제를 봤을 때 떠올릴 수 있는 전략은 일종의 parametric search를 수행하는 것이다. 가장 큰 자릿수부터 시작하여 점점 자릿수를 내려간다. 각 위치가 $9, 8, \cdots, 1$일 때, 남아있는 안쪽의 수들에 코크를 적당히 배치하여 팰린드롬수가 되는 경우가 존재하는지 판별한다. 핵심은 이 가능성 판별 작업을 어떻게 수행할 것인지이다.

가장 큰 자릿수인 $9$를 생각하자. 최대라는 조건을 활용하여, 항상 $9$를 배치하는 것이 강제되는 자릿수 위치들을 먼저 생각해보자. 어떤 대칭적인 위치의 문자 $S_i$와 $S_{n+1-i}$ 중 하나가 $9$이고 다른 하나는 $9$가 아니라고 하자. 그러면 $9$가 아닌 쪽은 최종 답에 무조건 $9$인 상태로 끝나야 한다. 이미 입력에서 주어진 값보다 작은 상태로 진입하는 것이 불가능하기 때문이다. 그러므로 크기 $9$짜리 파란 코크를 무조건 $1$개 사용해서 $9$가 아닌 쪽을 $9$로 만들어야 하므로, 입력이 $9$였던 위치의 크기 $9$ 파란 코크를 가져오고, 파란 코크가 하나 예비로 남는다. 비슷하게 $S_i = S_{n+1-i} = 9$였으면 이미 조건이 만족되었고, 이를 다른 자릿수로 바꿀 수도 없으므로, 크기 $9$ 파란 코크가 $2$개 예비로 남는다.

이 과정을 거치면 1) 크기 $9$짜리 코크가 몇 개 예비로 남게 되며, 2) 아직 고정되지 않은 위치들은 전부 $9$가 아닌 수들만 구성된다. 이제 위에서 설명한 parametric을 약간 변형하여, 맨 앞 자리(와 그에 대칭되는 위치)들을 몇 개까지 $9$로 채울 수 있는지를 따질 것이다. 이것은 앞서 설명한 1번/2번 성질에 의해 $9$ 코크가 남은 만큼 채워나가면 된다. 따라서 자릿수가 가장 큰 위치인 $(S_1, S_n), (S_2, S_{n-1}), \cdots$ 순서로 크기 $9$ 코크를 배치하고 원래 존재하던 코크를 예비용으로 바꾼다. 그러므로 이 작업이 끝난 이후 $9$와 관련된 모든 정보는 결정되었으므로, 나머지 위치들에 대해 같은 작업을 자릿수 $8, 7, \cdots, 1$에 대해 반복해주면 된다.

약간 미묘한 점은, 예비로 남은 $9$ 코크를 개수가 소진될 때까지 배치하는 작업을 끝내고 나면, 그 상태에서 남은 자리들에 코크를 잘 배치해서 팰린드롬수를 만들 수 있는 여지가 항상 남아있는가? 라는 질문이다. 생각해보면 이건 당연히 되는 게, 아직 결정되지 않은 자리들은 무조건 대칭적이기 때문에, $N = 2$인 subproblem 여러 개가 남아 있는 상황으로 약화시킬 수 있고, 그러므로 팰린드롬수로 만들 가능성은 남아 있게 된다.

괄호 문자열은 버거인가?

답에 대한 이분 탐색이 가능함을 먼저 확인하자. 그러므로 사용한 기계의 대수를 $\theta$로 두고 결정 문제를 푼다. Greedy 전략은 상당히 단순한데, 가장 먼저 들어온 요청을 먼저 처리하는 방식이 항상 이득임을 알 수 있다. 증명은 exchange argument로 바로 가능. 그러므로 각 $\theta$마다 시뮬레이션을 돌려서 실제로 가능한지 아닌지 판별하면 된다.

흔히 하는 점들의 정렬 - $x$좌표 순서, 그 다음 $y$좌표 순서 - 로 점을 정렬해두자. 이제 첫 번째 점을 잡고, 이 점을 포함하는 정사각형을 찾을 것이다. $2$차원 상에서 이 점은 다른 모든 점들을 바라봤을 때, 그 시야가 180도보다 작다는 성질을 갖는다. 그러므로 이 점을 포함하는 정사각형은, 이 점보다 $y$좌표가 작거나 같은 방향의 인접한 점을 하나 선택하면 유일하게 결정된다. (나머지 점 $2$개가 있을 위치에 점이 없다면 존재하지도 않겠지만) 귀류법(?)으로, 이 점을 포함하는 정사각형의 후보가 $2$개 이상이라고 하자. 그러면 다시금 시야가 180도보다 작다는 성질 때문에, 두 정사각형 영역이 분리되어 있을 수는 없고, 따라서 정사각형 후보 중 변 길이가 더 작은 쪽의 점이 다른 후보 영역에 포함된다. 이는 입력 조건 상 모순이므로, 또한 항상 답이 존재하는 입력이 주어지므로, 결국 이 점을 포함하는 정사각형의 유일한 후보는 모든 정사각형 중 최소 변 길이를 갖는 $4$개의 점 조합이다. 반복적으로 이러한 정사각형을 제거해주면 $O(N^2 \log N)$에 문제가 해결된다. 아무 생각 없이 map 같은 걸 쓰면 상수가 좀 빡빡해보이니 (왜냐면 실제 입력이 $4N$개이므로...) 적당히 잘 구현하기.

문제를 읽고 든 생각이 $2$개가 있다. 1) 이 포스팅을 시작할 때까지만 해도, 그리디와 기하가 섞인 문제의 존재성은 생각도 안 해서 슬펐다. 2) '이게 답이 유일하다고?'였다. 앞의 풀이에서 정렬했을 때 최소인 점을 생각하는 게 생뚱맞을 수 있는데 (물론 다른 기하 문제에서 많이 사용하긴 한다), 필자는 두 번째 생각에 대해 반례를 찾으려고 시도하다가 motivation을 얻었다. 보통 답의 유일성에 대해 논할 때는, 혹은 유일하지 않다는 것에 반례를 잡으려고 할 때는, 뭔가 생각을 시작할 만한 object가 필요하다. 이 생각만큼은 좀 하늘에서 떨어진 아이디어로 시작하긴 했는데, 답을 구성하는 정사각형 중 최소 크기인 것으로 출발했다. 그래서 점 개수가 $10^3$ scale이므로 임의의 두 점을 잇는 선분을 전부 확인하는 작업이 가능하기 때문에, 이들을 길이 순서대로 보면서 정사각형이 만들어질 수 있는지 체크하면 되지 않을까 같은 생각을 했다.

다만 이 방향성으로 생각하면, 예를 들어 $N = 4$일 때 $100 \times 100$ 크기 정사각형이 $201 \times 201$ 크기 정사각형에 잘 들어가 있는 점 배치에서 뭔가 문제가 생긴다. 안쪽에 $1 \times 1$ 크기를 이루는 점 $4$개가 있는데, 이걸 무작정 정사각형 중 하나로 간주해버리면 다른 정사각형들이 만들어지는 순간 영역을 침범하기 때문이다. 그래서 이 반례가 '안쪽'에 배치된 점에서 기인한다고 생각해서 위 풀이와 같은 아이디어를 잡을 수 있었다.

다른 시리즈들 입력은 안 열어봤지만, 이 문제만 입력이 특이해서 쉽게 풀 수 있다. 열어보면 알겠지만, $100 \times 100$ 격자에서 오른쪽 위 점이 딱 하나만 없는 입력이다. 문제 조건 상 삼각분할이 항상 가능하다고 말하고 있으므로, 최종 결과는 maximal planar graph이고, $e = 3v-6$을 항상 만족함을 보일 수 있다. 따라서 $e$는 고정된다. 문제에서 주어지는 모든 입력 좌표는 정수이므로, 길이 $1$짜리 간선을 고를 수 있는 대로 고르자. 이 개수가 $e$보다 약간 모자란데, 정확히 그 다음으로 가능한 짧은 길이 $\sqrt{2}$를 서로 대각선끼리 안 겹치게도 고를 수 있다. (이 개수는 정확히 $100 \times 100$개이다) 그러므로 이것이 가능한 최솟값.

가장 먼저 할 수 있는 생각은 칸을 사전순으로 보면서, 켜진 칸 $(x, y)$가 있으면 그 칸을 모서리로 하는 직사각형을 사용하는 것이다. 그러면 다른 쪽 모서리를 어떻게 결정할 것인지만 생각하면 되는데, 아마 다음의 두 전략이 자연스럽다.

1. 오른쪽으로 연속한 켜진 칸 구간만큼 전진 (즉 $(x+\Delta x, y)$), 위쪽으로도 마찬가지로 전진. 직사각형 크기는 $\Delta x \times \Delta y$.

2. $(x, n-1)$에서 $y$좌표를 아래로 훑으면서 최초로 켜진 칸을 발견하면 멈춤. $(n-1, y)$에 대해서도 똑같은 작업을 해주고, 멈춘 위치를 모서리들로 갖는 직사각형을 사용.

이들 중 이 테스트케이스는 $1$에서는 안 되고, $2$에서는 $1200$개 정도로 잘 된다. 참고로, 각각은 최적 전략이 아니다. 저러한 전략에 어긋나는 최악의 입력은 잘 생각해보면 많다. 예제만 봐도 $2$번 전략은 별로 좋지 않다.

$x_i$, $y_i$, $z_i$를 각각 $i$번째까지 문자를 읽었을 때 가장 적게 등장한 문자의 등장 횟수, 두 번째 빈도, 가장 많이 등장한 문자의 등장 횟수라고 하자. 그러므로 $x_i \leq y_i \leq z_i$이고 $x_i + y_i + z_i = i$이다. 이 때 이 문제의 답이 $\max_{i=1}^n (z_i-x_i)$임을 보일 것이다.

증명은 구성적으로 할 수 있다. 한 글자씩 차례대로 읽으면서, 문자열들을 여러 개로 나누는데, beautiful string이 되는 순간 세 글자를 묶어서 제거한다. 정확히는 어느 시점에 아직 묶여서 제거되지 않은 문자열들이 몇 그룹 존재할 때, 내가 현재 읽은 문자가 들어있지 않은 그룹 중 하나를 선택해서 합친다. 그러한 그룹이 없으면 새로운 공간(문자열 그룹)을 만든다. 이러한 전략은 문자열을 처리하는 과정 중에 아직 제거되지 않고 남아있는 문자열의 개수가 최대인 시점의 개수만큼 subsequence partition을 요구한다. 또한 입력 조건 상 모든 문자의 개수가 같다는 조건 때문에, 모든 문자를 읽고 처리한 시점에 묶이지 않고 남아 있는 문자열이 없음을 보장한다.

처음에 보이고 싶었던 명제와 이러한 성질들은 전부 다음의 성질이 귀납적으로 성립함을 보임으로써 해결 가능하다: $i$번째 시점에, $z_i$에 해당하는 문자만 정확히 하나 들어있는 그룹들이 $z_i-y_i$개 존재하며, $y_i$와 $z_i$에 해당하는 문자가 들어있는 그룹들이 $y_i-x_i$개 존재한다. 따라서 총 $z_i-x_i$개 그룹이 존재한다. 증명은... case work로 매우 straightforward하게 보일 수 있으니 생략.

$k = 1$인 경우, 모든 점들을 채굴하기 위한 최소 비용은 $(\max_{i=1}^n y_i - \min_{i=1}^n y_i) / 2$이다. 가장 $y$좌표가 큰 지점과 작은 지점 두 곳을 고려하면 쉽게 증명할 수 있다. 답에 대한 이분 탐색이 가능하므로, $\theta$의 cost로 $k$개의 구간을 찾을 수 있는지 확인하자. 이제 $p_1$부터 $p_t$까지를 $\theta$의 cost로 처리할 수 있다고 하자. 어떤 점들을 채굴하기 위한 비용은, 그 점들의 부분집합을 채굴하기 위한 비용보다 항상 같거나 크다. 왜냐하면 동일한 구간 분할을 재활용했을 때 답이 최악의 경우 그대로이고, 감소하기만 할 수 있다. 따라서 $p_1$부터 $p_t$까지 처리할 수 있다면 $p_1$부터 $p_{t-1}$까지도 처리할 수 있는데, 나머지 구간 $p_{t+1}$부터 $p_n$까지 처리하는 비용이 $p_t$부터 $p_n$까지 처리하는 비용보다 항상 같거나 크므로, 우리가 관심 있는 값은 $t$의 최댓값이다. 그러므로 점을 순서대로 읽어나가면서 $\theta$의 cost로 처리 가능한 최대 길이의 구간을 잘라내는 과정을 반복하여, $k$개 이하의 구간을 잘라내었는지로 이분 탐색을 진행하면 된다.

$(T_1, S_1)$과 $(T_2, S_2)$ 작업을 순서대로 진행한다고 할 때, 이것이 $(T_2, S_2)$ 다음에 $(T_1, S_1)$ 작업을 진행하는 것보다 이득일 조건을 생각해보자. 전자의 경우 $2$번 작업을 나중에 시작하여 생기는 보상금은 $T_1 S_2$이고, 후자의 경우의 보상금은 $T_2 S_1$이다. 그러므로 $T_1 S_2 < T_2 S_1$이어야 $1$번 작업 후 $2$번 작업을 진행하는 것이 이득이며, 역도 성립한다. 따라서 작업이 $n$개 있어도 $S/T$ 값이 큰 작업부터 진행하는 것이 이득이라는 추정을 할 수 있고, 실제로 성립한다. 왜냐하면 위의 논의에서 인접한 두 작업 외에 존재하는 $n-2$개의 작업들은, 두 작업의 배치 순서에 관계 없이 동일한 보상금이 필요하기 때문이다. 따라서 위의 정렬 기준에 맞춰서 작업들을 정렬하는 것으로 해결 가능.

Exchange argument를 사용하는 대표적인 유형이다. 일반적으로 순서를 정하거나, 배열을 해야 하는 (늘어놓기) 문제들은 이러한 분석으로 풀리는 경우가 많은데, 사실 이 방법 이외에는 분석의 시작점이 되는 수학적 구조가 별로 없어서 exchange argument를 사용하겠다 정도의 느낌으로 풀게 되는 경우가 많은 것 같다.

각 팀이 문제를 여러 개 맞출 수 있지만, 그냥 여러 개의 팀이 전부 하나의 문제만 맞춘다고 바꿔서 생각해도 문제 없다. 먼저 capacity 조건을 무시하고, 모든 풍선이 $A$ 쪽에서 온다고 하자. 이들 중 몇 개를 적당하게 골라 $B$쪽에서 오도록 바꾼 것이 최적해일 것이다. 그러면 모든 풍선을 $A$에서 가져올 때의 비용을 $X$, $i$번째 풍선을 $B$에서 가져오기 위해 추가로 지불해야 하는 비용을 $\Delta_i$라고 하면, 이 문제는 결국 $\Delta$ 값들 중 $n-b$개 이상 $n-a$개 이하를 골라 이들의 합을 최소화하는 문제로 바뀐다. 그러므로 $\Delta$를 정렬하고 먼저 $n-b$개를 작은 순서대로 고르고, $0$보다 작은 값이 나올 때 멈추거나 $n-a$개를 고르면 멈추면 된다.

이원화된 cost가 있는 문제를 자주 볼 수 있는데, 그 중에서 가장 쉬운 형태인 것 같다. 먼저 선택을 한 쪽으로 강제하고, 조건에 만족시키기 위해서 $\Delta$로 계산을 하는 테크닉 자체도 자주 나온다. 또 이런 유형을 플로우 모델링의 관점에서 볼 수도 있다. 실제로 플로우를 돌려서 문제를 풀 수 있는 경우가 있는지는 모르겠음. 이 문제와 관련이 얼마나 있는지는 모르겠으나, 느낌상 비슷한 문제를 찾자면 이거, 이거.

직관적으로 비용이 큰 행/열을 먼저 잘라야 하는 게 이득이다. 이에 따라 가장 큰 비용이 필요한 행/열을 자른 다음, 두 번째로 큰 비용은 반대 방향이라고 하자. 이 때 갈린 판 각각은 서로 독립으로 변하고, 이에 따라 두 번째로 큰 비용이었던 행/열이 다시 가장 큰 비용이 되므로, 결국 전체 판의 관점에서 보면 항상 행/열을 통째로 자른다고 생각해도 된다.

그렇지만 이걸 증명할 방법은 모르겠어서, 풀 때는 위의 notion만 가지고 방식 자체는 다르게 풀었다. 문제를 반대로 생각해서, 모든 square를 다 자르기 위해서 각 square의 side마다 비용을 지불했다고 하자. 한 번에 자르면 비용을 여러 번 지불할 필요가 없었으므로, 이 조건을 어떻게 적용할 것인지 생각해보자. 어떤 교차점을 지나는 행/열이 각각 $x_i$, $y_j$ 비용을 지불하는 행/열이라고 하자. 이 때 이 교차점은 행이나 열 중 하나를 선택하여 비용을 $x_i$ 또는 $y_j$만큼 절약할 수 있다. 교차점을 없애고 양쪽의 행이나 열 중 하나를 merge한다고 생각하면 된다. 따라서 이러한 과정을 $(m-1)(n-1)$개의 교차점에서 전부 시행했을 때 절약할 수 있는 최대치는 다음과 같다. $$ \sum_{i=1}^{m-1} \sum_{j=1}^{n-1} \max(x_i, y_j) $$

마지막으로 살펴봐야 하는 건 위의 답을 만족하게 교차점에서 행/열의 잘린 조각들을 merge했을 때, 시작할 때의 초콜릿 판에서 시작하여 실제로 그렇게 자르는 방법이 있냐는 것이다. 이것이 맨 앞에서 설명했던 notion을 사용하는 지점이다. 가장 비용이 큰 행/열을 생각하면 항상 $\max$ 값이 그 행/열을 가리킬 것이므로, merge가 일어난 이후 그 행/열은 전부 하나로 합쳐지고, 이는 전체 판에서 처음 잘릴 행/열을 나타내게 된다. 그 이후로는 계속 subproblem이 되는 셈이므로, ok.

먼저 조건 $1$을 완화해보자. 박스를 트럭에 실은 후 아무 곳에나 내릴 수 있되, 그 박스가 원래 향하는 목적지가 아니면 전달하지 못한 것으로 간주한다고 해도 무방하다. 어차피 배송 용량 조건은 남아 있기도 하고, 목적지에 도달하지 못하고 중간에 내린 박스는 애초에 처음부터 선택하지 않은 것으로 취급해도 다른 조건에 위배되지 않기 때문이다. 또한, $a \leq b \leq c \leq d$에 대해, $a$에서 $d$로 향하는 박스와 $b$에서 $c$로 향하는 박스가 있다고 할 때, $[b, c]$ 박스가 제대로 배달되지 않으면서 $[a, d]$ 박스는 제대로 배달되는 최적해가 존재한다면, 이 둘의 배달 여부를 바꿔서 $[b, c]$를 배달하고 $[a, d]$를 포기한다고 해도 해가 더 나빠지지 않는다.

이제 맨 처음 시작점에서 트럭에 실을 최대 $C$개의 박스를 생각하자. 위의 논리에 따르면, 시작점에서 출발하는 박스가 $C$개보다 많다면 도착점이 작은 박스부터 실어야 함을 알 수 있다. 그게 아니라면 애초에 트럭에 전부 실을 수 있다. 이렇게 하여 $2$번 지점에 도착했을 때, 박스의 상하차가 자유롭도록 조건을 완화시켰으므로 일단 모든 박스를 내리고 보자. $2$번 지점이 도착점인 박스는 이 순간 무사히 배송된 것이다. 그리고 그렇지 않은 박스들은, 이미 배송되어 버린 이상 + 트럭이 뒤로 돌아가지 않으므로, $2$번 지점이 새로운 시작점이 된 박스들로 취급해도 무방하다. 따라서 방금 전의 논리처럼, 시작점 다음으로 향할 때 실을 박스들은 도착점이 작은 순서대로 실어야 한다고 했으므로, 이러한 greedy 과정을 반복하는 게 항상 최선이다.

이 과정을 high-level view에서 다시 서술하자면, 각 마을에서 박스를 트럭 용량이 넘치기 전까지 도착점이 가까운 순서대로 싣되, 용량이 전부 넘친 상황에서 현재 트럭에 실린 박스가 싣지 못한 짐보다 도착점이 먼 경우 그 둘을 교체하면서 박스를 운송한다와 동치이다.

우선 이벤트들 중 요구하는 능력이 최대인 이벤트를 능력 별로 찾은 후, 최소한 그만큼은 score를 올릴 수 있는지 판별해야 한다. 이것이 이벤트를 모두 마칠 수 있는가 아닌가에 대한 필요충분조건인 것은 자명. 이제 남은 point를 $1$점씩 사용해서 적절하게 능력치를 증가시키다보면 어떤 최적해에 도달할 수 있을 텐데, 그러므로 $f_i(x)$를 $i$번 score를 $x$점만큼 올렸을 때 최종 점수 증가량이라고 정의하자. (최소 요구량을 맞춘 이후에 추가로 $x$점을 올렸다는 의미)

이제 각 능력 별로, 필요한 능력 score 최대치와 현재의 score가 정확히 같은 경우와, 초기 score가 애초에 요구 조건보다 컸던 경우 두 가지로 나뉜다. 첫 번째 경우 $f_i(1) > f_i(2)$일 텐데, 왜냐하면 처음 올리는 $1$점은 여유롭게 클리어하는 이벤트를 새로 만들기 때문이다. $f_i(2)$부터는 그 능력을 요구하는 이벤트의 개수만큼의 증가량을 가지며, 따라서 $f_i(2) = f_i(3) = \cdots$이다. 두 번째 경우는 초기에 올리는 점수가 딱히 특별하지 않으므로, $f_i(1) = f_i(2) = \cdots$를 만족한다. 따라서 $f_i(2) = f_i$라고 두면, 최소한 $F = \max_{i=1}^n f_i$만큼의 점수를 능력 score $1$점 당 획득할 수 있게 되며, $f_j(1) > F$인 모든 $j$를 먼저 얻으려고 시도하면 된다.

꽤 전형적인 유형의 문제다. 어떤 간선이 lowest value가 되는 component를 생각해보자. 이들 중 크기가 최대인 것은, 그 간선으로부터 bfs 비슷한 걸 돌려서 이 가중치 이상인 간선만 사용해서 갈 수 있는 범위의 component이다. 따라서 관점을 바꿔서 간선의 가중치를 내림차순으로 정렬한 뒤 그 순서로 간선을 초기에 간선이 없던 forest에 추가한다고 생각하자. 이러면 간선이 추가되는 순간마다 그 간선을 lowest value로 갖는 최대 크기 component는 추가되는 순간 그 간선이 포함된 component와 같다. (사실 가중치가 같은 간선이 있으면 정확히 맞는 말은 아닌데, 이 경우에는 그들 중 마지막으로 추가되는 간선만 고려해도 된다) 그러므로 union-find로 이러한 과정을 관리해주면 된다.

문제에서 necklace decomposition의 존재성을 보장해줬기 때문에 문제를 비교적 쉽게 풀 수 있다. 주어진 문자열의 necklace decomposition에서 첫 번째 문자를 포함하는 necklace를 알아낼 수 있다면, 이를 문자열에서 제거하고 남은 문자열에서 같은 과정을 반복함으로써 문제를 해결할 수 있다. 이제 보이고 싶은 것은, 알아내고 싶은 그 necklace가 첫 번째 문자를 포함하는 가장 긴 necklace라는 것이다.

증명은 아직 모른다. 아래 참조.

이 문제는 Lyndon Factorization와 관련된 문제이다. 엄밀히 말하면 대소 비교에서 등호 처리가 lyndon word, lyndon factorization과 다르긴 하나 메인 로직 자체는 비슷할 것으로 추정된다. Lyndon factorization은 임의의 문자열에 대해서 존재하고, 심지어 유일함이 증명되어 있다. 그러므로 이 증명을 찾아보면 위의 그리디 전략에 대한 증명도 찾을 수 있을지 모른다.

문제의 notation을 그대로 가져온다. 먼저 쉽게 관찰되는 것은, $s[t_k+1 .. n]$는 최적해에 포함되지 않아야 한다는 것이다. 이제 문자열을 거꾸로 읽으면서 문제를 해결할 것이다. $s_{t_k}$가 필수로 사용되어야 하고, 이것은 위의 관찰에 따라 최적해의 suffix여야 한다. 여기서 $s_{t_k-1}$번째 문자가 최적해에 포함될지 아닐지를 판별할 것이다. $[1, t_k - 2]$번째 문자들을 조건에 맞게 선택한 임의의 결과를 $A$라고 하자. 그러면 $s_{t_k-1}$의 사용 여부에 따라 $A s_{t_k-1} s_{t_k}$와 $A s_{t_k}$ 두 개의 후보가 생기는데, 이들의 대소 관계는 $A$에 무관하다. 즉 $s_{t_k-1} s_{t_k} < s_{t_k}$이면 최적해에서 $s_{t_k-1}$는 항상 사용되며, 반대라면 사용되지 않을 것임을 알 수 있다.

이러한 과정은 재귀적으로 반복될 수 있다. 즉 문자열을 거꾸로 읽어나가면서 최적해의 suffix가 되어야 할 subsequence를 알고 있으므로, 위의 논리를 그대로 적용할 수 있다. 즉 suffix가 되어야 할 부분을 $B$라고 하면 $AcB < AB \Longleftrightarrow cB < B$인지 판별하는 과정을 반복하면 되는 것이다. 이 작업은 문자열의 새로운 문자 $c$를 읽을 때마다 $O(1)$에 판별할 수 있다. $B$를 앞에서 뒤로 볼 때 가장 처음 등장하는 문자와 두 번째로 등장하는 문자를 각각 $x$, $y$라 하자. 이 때 $x$가 $B$의 prefix에서 몇 개나 사용되었는지에 상관없이, $cB < B \Longleftrightarrow cxy < xy$임을 쉽게 확인할 수 있다. $x$와 $y$는 $B$의 앞에 새로운 문자가 추가되어도 update가 바로 가능하므로 ok. 최적해를 이와 같이 구성해나가는 동안 주어지는 index sequence 위치의 문자는 비교 과정 없이 무조건 suffix에 사용되어야 하므로 $B$에 추가되어야 함을 유의해주면 된다.

추가할 단어 중 하나를 $S$라고 하면, $S$에서 마지막 글자를 뗀 단어는 $S$를 만들 수 있던 사전의 단어로부터 만들어질 수 있으면서, 더 많은 사전의 단어로부터 만들어질 가능성도 가지게 된다. 따라서 길이가 $2$ 이하인 단어가 총 $26 + 26^2$개 존재하고, 이것이 $n$의 최댓값보다 크므로, 최적해는 전부 단어 길이가 $2$ 이하인 단어들로만 구성되어 있다고 생각할 수 있다. 따라서 원래 사전에 있던 단어를 제외하고, 각 단어들이 만들어질 수 있는 사전의 단어 개수를 세어 값이 큰 순서로 $n$개를 답으로 출력하면 된다.

여러 자잘한 관찰이 필요하다.

1. 먼저 $n$을 입력 그대로 작성해도 최대 길이가 $8$이 되게 할 수 있다. $n = 10^8$이면 10 4 ^을 써서 길이를 줄일 수 있다. 따라서 $n$을 그대로 쓰는 경우가 아니라면, 최대로 사용할 수 있는 연산은 $3$개이다. $4$개 이상의 연산자를 사용하면 $5$개 이상의 피연산자가 필요하므로 최소 길이가 $9$ 이상이 되기 때문이다.

2. 연산자를 사용하는 경우, 가장 먼저 실행되는 연산이 *라고 가정하자. 이 경우 a b *가 $ab$로 변하는데, $a$가 $k$자리 수이고 $b$가 $l$자리 수라고 했을 때 $a < 10^k$, $b < 10^l$이므로 $ab < 10^{k+l}$이 되어 $ab$는 최대 $k+l$자리 수이다. 따라서 a b *라는 식을 쓸 때 이미 길이가 $k+l+1$이므로 첫 연산이 곱하기이면 이를 곱한 결과로 대치하는 게 항상 이득이다. 그러므로 첫 연산은 항상 ^이다.

3. ^ 연산의 결과가 다른 연산의 피연산자로 들어갈 때, 그 연산이 ^라고 가정하자. 즉 $a^b$가 다른 피연산자 $c$와 ^로 연결되면 ${a^b}^c$ 혹은 $c^{a^b}$가 된다. 여기서 $a^b < 10^3$이었다면, a b ^가 최소한 길이가 $3$ 이상이므로 $a^b$의 결과를 그대로 사용하는 게 더 낫다. 따라서 $a^b \geq 10^3$으로 가정할 수 있다. $c = 1$이면 어떤 경우에도 ^을 하지 않는 게 이득이므로 $c \geq 2$인데, 따라서 후자의 경우 계산 과정 중에 $2^{1000}$을 이상인 수가 나오므로 입력 범위 상 불가능. 전자의 경우 ${a^b}^c = a^{bc}$이므로 앞선 관찰에서와 같이 곱셈 결과를 그대로 쓰는 게 더 이득이다. 따라서 ^의 결과로 나온 값들은 바로 연속해서 ^의 피연산자로 쓰일 수 없다.

위의 경우를 종합하면, 정답으로 가능한 식은 다음의 $4$가지 뿐이다.

• a
• a b ^
• a b * c ^
• a b ^ c d ^ *

거듭제곱을 하려고만 해도 밑이 $10^4$인 경우 이외에는 고려할 필요가 없다는 등의 관찰을 통해서, 탐색 범위가 $O(n^4)$까지 치솟지 않음을 확인할 수 있다. 다양한 커팅이 존재하고 웬만하면 다 돌 것이다. 다만 맞은 사람 목록을 보면 이러한 그리디 풀이가 아니라 dp를 쓰는 게 더 빨리 작동한다.

증명을 아직 못 찾았다.

$k$번째 라운드에 보이는 숫자들을 $a_1 \leq a_2 \leq \cdots \leq a_k$, $b_1 \leq b_2 \cdots \leq b_k$라고 하자. 이 때 여기서 쓸 수 있는 전략은 $a_i$와 $b_{k+1-i}$를 매칭시키는 것이다. 전형적인 유형이고, 증명도 꽤 쉬운 편이다. $a_i$와 매칭된 수를 $b_{\pi(i)}$라고 하자. 이 때 $i < j$이고 $\pi(i) < \pi(j)$인 경우가 존재한다면, $\max(a_i + b_{\pi(i)}, a_j + b_{\pi(j)}) \geq \max(a_i + b_{\pi(j)}, a_j + b_{\pi(i)})$이기 때문에 이 둘의 매칭을 바꿔주는 게 항상 이득이다. 따라서 최적해는 최소한 $\pi(x)$가 $x$에 대해 감소하는 함수인 경우이고, 이러한 경우는 오직 앞에서 제시한 전략뿐이다.

이에 따라서 실제로 매 라운드마다 수를 찾는 작업은 $A, B \leq 100$이라는 점을 이용하여, 라운드가 아무리 많이 진행되어도 결국 $(a_i, b_{k+1-i})$ pair는 중복이 많다는 사실을 이용하면 된다. 이들은 아무리 많아야 $199$종류만 관찰될 수 있기 때문이다. 서로 다른 pair는 첫 번째, 두 번째 원소 중 최소 하나가 다르다는 의미인데, $i$가 $1$에서 $k$까지 증가하는 동안 첫 번째 원소는 최대 $99$번만 증가하고, 두 번째 원소도 최대 $99$번만 감소하기 때문. 구현의 측면에서는, two pointer로 정보를 관리해줄 수 있다.

어떤 순간에 수열을 $A_i$라고 하고, $d_i = A_i - A_{i-1}$이라고 하자. 즉 최종 상태는 어떤 $1 \leq k \leq n$이 존재하여, $2 \leq j \leq k$에 대해 $d_j > 0$이고 $k < j \leq n$에 대해 $d_j < 0$를 만족하는 상황을 원한다. $d$를 정의하는 것이 좋은 이유는, 구간에 $+1$을 하는 operation이 어떤 $d$의 두 위치를 잡아 왼쪽에 $+1$, 오른쪽에 $-1$을 하는 연산으로 바뀌기 때문이다. 경계에 걸쳐서 operation을 사용한다면 아무 위치 한 곳에 $+1$ 또는 $-1$을 할 수도 있다.

이제, 최종 상태에서 $d$가 $d_k$부터 음수라고 하자. Operation은 한 번에 최대 하나의 수를 증가시킬 수 있다. (혹은 감소) 그러므로 $k < j \leq n$에 대해 $d_j$가 모두 음수가 되기 위해 필요한 operation은 최소한 $\sum_{j=k+1}^{n} \max(0, 1+d[j])$이며, 비슷한 원리로 $2 \leq j \leq k$에 대해 $d_j$가 모두 양수가 되기 위해서는 $\sum_{j=2}^{k} \max(0, 1-d[j])$만큼이 필요하다. 수를 증가/감소시킬 위치는 자유롭게 선택 가능하다. ($k$를 기준으로 왼쪽은 항상 수를 증가시키기만 하면 되고, 오른쪽은 감소시키기만 하면 되므로, operation을 사용할 때 위치 제약이 없는 것이나 다름 없다) 따라서 $k$를 고정하지 않는 전체 문제의 답은 다음과 같다. $$ \min_{k=2}^{n} \max( \sum_{j=k+1}^{n} \max(0, 1+d[j]), \sum_{j=2}^{k} \max(0, 1-d[j])) $$

이는 사전에 $d$ 배열을 전처리해서 각 $k$마다 필요한 값을 계산해놓을 수 있다.

이게 왜 그리디인지 모르겠으나, 일단 내 풀이를 적어두긴 하겠다. 결국 직사각형 $2$개로 분할되려면, 어떤 두 직사각형 사이를 지나는 분리선이 존재해야 한다. 이러한 가능한 분리선은 총 $m+n$가지 정도 있고, 각각의 나뉜 영역에서는 온전한 직사각형 $1$개가 존재하는지 판별하는 작업을 거치면 된다. 이 작업은 각 영역에서 점을 순서대로 읽었을 때 직사각형의 양 대각선 끝점이 될 위치, 즉 일종의 사전순 최소로 칠해진 지점과 최대로 칠해진 지점을 구하고 그 사이가 전부 채워져있는지 판단하면 된다. 다른 위치에 칠해진 타일이 없나도 체크해주면 ok. 따라서 시간복잡도는 $O(mn(m+n)$.

먼저 한 종류의 동전은 양쪽이 $1$개 이상 주고받지 않아도 된다. 그렇다면 그냥 서로 주고받지 않는 게 더 적은 교환을 만들기 때문이다. 또한 그 다음 관찰은 $10$개 이상 같은 동전을 사용할 필요가 없다는 것이다. 한쪽 방향으로 $10$개를 줄 바에 더 큰 단위 $1$개를 주는 게 낫다. 이러한 관찰 하에서 얻어지는 또다른 결과가 있다. 지불할 금액의 $1$의 자리가 $r$일 때, $1$원 동전은 $r$개를 지불하거나 $10-r$개를 미리 받는 경우뿐이다. 따라서 $0 \leq r \leq 4$이면 $r$개를 지불하는 것이 이득이고, $6 \leq r \leq 9$이면 받아올림을 하고 미리 동전을 $10-r$개를 받는 게 이득이다. 예를 들어 지불할 금액 $N = \overline{x6}$인 경우를 생각하자. $n$을 지불하는 최적의 교환 횟수를 $f(n)$이라고 표기하자. $r = 6$원을 그대로 지불하면 $6$개를 사용하지만 받아올림을 쓰면 총 $5$번의 교환으로 해결되기 때문이다. 따라서 $f(x)+6 \geq f(x+1)+5$를 만족할 것이므로 결과가 최소한 더 나빠지지는 않는다. 왜냐하면 $|f(x+1)-f(x)| \leq 1$이 항상 성립하기 때문.

남은 경우는 $1$의 자리가 $5$인 경우이다. 지불할 금액이 $N = \overline{xa5}$일 때 ($a$가 한 자리 수) 그리디 전략은 다음과 같다. $0 \leq a \leq 4$이면 $5$원을 그대로 지불, 아니면 받아올림하여 $5$원을 미리 받는 것이다. $0 \leq a \leq 4$인 경우 귀류법을 사용하면 $f(\overline{xa})+5 > f(\overline{x(a+1)})+5$라는 것인데, 앞선 관찰에 따라 $f(\overline{xa}) = f(x) + a$이다. 따라서 $f(\overline{x(a+1)}) = f(x) + a+1$일 수는 없으므로 $f(\overline{x(a+1)}) = f(x+1)+10-(a+1)$인데, $f(x) \leq f(x+1)+1$이기도 하므로 모순. $6 \leq a \leq 9$인 경우에도 $f(\overline{xa})+5 < f(\overline{x(a+1)})+5$로 귀류법을 사용하면, $f(\overline{xa}) = f(x+1) + 10-a$이고 $f(\overline{x(a+1)}) \leq f(x+1) + 10-(a+1)$이므로 모순. 마지막으로 $a = 5$인 경우는 $f(\overline{xa}) = \min(f(x), f(x+1)) + 5$이므로, 같은 방식으로 귀류법을 쓰면 $\min(f(x), f(x+1)) < f(x+1)-1$가 되어 모순.

밑의 풀이는 증명은 아니고, 증명 같아 보이는 무언가인데, 나중에 시간 나면 보강해보도록 하겠다.

직관적으로는 $B$에 가까운 버팀목 조합을 만들고, 마지막에 $B$ 이상인 버팀목들을 크기 순으로 사용하는 것이 이득일 것이다. $p_i \geq B$인 버팀목은 다른 버팀목과 조합할 필요가 없으므로, $2$개까지 사용할 수 있다는 조건은 $p_i < B$인 버팀목들에만 적용하면 된다. $1$짜리 버팀목을 생각해보면, 이 버팀목은 $B-1$짜리 버팀목과 조합하는 게 아닌 이상 사용되지 않는다. 따라서 먼저 이들을 조합해준다. $B-1$짜리가 $1$이 아니라 다른 크기 $x$와 조합하는 것이 최적해였다면, $x$를 $1$로 대체하는 게 항상 이득이기 때문이다. 따라서 이제 그 다음으로 작은 버팀목은 $2$인데, 이들은 먼저 $B-2$짜리와 조합한 후, 여전히 개수가 남아 있으면 $B-1$과 합치는 게 이득이다. 위의 논리 (exchange argument)를 반복적으로 적용하면 이러한 결론이 나오는 이유를 알 수 있다. 이후 계속해서 $3$짜리, $4$짜리를 이런 방식으로 합쳐주고 만들어진 $B$ 이상의 버팀목들을 작은 것부터 사용해주면 최적이 된다. 최후에 만들어진 $B$ 이상의 버팀목 개수가 $N$ 이상인지 체크하는 건 덤.

구현의 측면에서, $B/2$ 이상인 버팀목은 같은 크기와 조합하는 걸 먼저 테스트하는 예외 처리가 필요할 수 있다.

Naomi의 수를 $a_i$, Ken의 수를 $b_i$로 쓰자. ($1 \leq i \leq N$) 먼저 War를 분석한다. Matching $M$을 다음과 같이 정의하자: $M = \{ (i, j) \mid a_i < b_j \}$. 그러므로 Maximum matching $M$이 존재하여, $|M|$이 Ken이 획득 가능한 최대 점수임을 보일 수 있다. $|M|+1$점을 획득 가능하다면 $M$이 maximum matching임에 바로 모순이다. $|M|$점을 획득하는 전략도 존재한다. Naomi가 제시한 블럭보다 무거운 블럭이 존재하면, Ken은 그 중에서 최소 무게인 블럭을 제시한다. 아니라면 현재 본인이 가진 블럭 중 최소인 것을 제시한다. 여기에서 문제의 지문에서 나온 문장인 '...and she knows Ken will always follow his unique optimal strategy for War, ...'에서 uniqueness가 주어졌다고 믿는 것이다. 다시 말해서, 이 전략이 $|M|$점을 획득하는 전략임을 증명하면 Ken의 행동을 완벽하게 서술한 것이다.

증명은 꽤 straightforward하다. $t$번째 라운드 이후 아직 사용하지 않은 블럭들의 집합이 $S_t = \{ \{ a_i \}, \{ b_i \} \}$이고, $S_t$에서 위와 같은 정의의 matching을 정의할 때 maximum matching의 크기를 $M_t$라고 하자. Ken이 $t$라운드 종료 후 얻은 점수를 $C_t$라고 할 때, $M_t + C_t = |M|$이 성립함을 보이면 된다. 이러면 $M_n = 0$임이 항상 보장되기 때문이다. Ken이 $t$라운드에 Naomi의 블럭을 이길 수 없는 블럭이 없었으면 $C_{t-1} = C_t$인데, 이 때 Naomi의 블럭은 임의의 Ken의 블럭보다 컸을 것이므로 Naomi의 블럭을 포함하는 maximum matching은 당연히 $S_t$에 존재하지 않는다. 한편 Ken이 위의 전략에 따라 블럭을 제시한 경우, $M_t = M_{t-1}-1$임을 보여야 한다. Maximum matching의 정의에 따라, $M_{t-1}$에서 $a < b$ 꼴의 pair를 하나 제거했는데도 matching의 크기가 $M_t = M_{t-1}$로 유지되는 것은 불가능하다. 또한 $S_{t-1}$에서 $S_t$로 가는 과정에서 사라진 값이 $2$개이므로, 이들이 전부 maximum matching의 일부로 관여했다고 쳐도 $M_t \geq M_{t-1}-2$는 만족한다. 그러나 Ken의 전략에 따르면 $M_t = M_{t-1}-2$는 불가능한데, $S_{t-1}$에서 maximum matching을 이루는 $a_{i_1} < b_{i_1}$과 $a_{i_2} < b_{i_2}$ pair가 $t$라운드에서 $a_{i_1} < b_{i_2}$가 Naomi와 Ken의 선택에 의해 사라졌다고 하자. Ken의 전략에 따르면 $a_{i_1} < b_{i_2} < b_{i_1}$이었을 것이므로, 여전히 $a_{i_2} < b_{i_1}$을 만족하여, $M_{t-1}$에서 $t$라운드에 의해서는 바뀌지 않는 $M_{t-1}-2$개의 matching과 $(a_{i_2}, b_{i_1})$ pair를 찾을 수 있으므로 $M_t \geq M_{t-1}-1$임을 보장할 수 있기 때문이다.

이제 Deceitful War (이하 DWar)를 분석하자. 예제가 나름 강력해서, 손으로 게임을 하다 보면 아이디어를 잡는 게 아주 어렵지는 않다. 핵심 관찰은, Dwar에서 Naomi가 얻을 수 있는 점수는 War에서 Naomi와 Ken의 역할이 바뀌었을 때 (단 수열은 서로 바꾸지 않은 채로) Naomi가 얻을 수 있는 점수와 같다는 것이다. 따라서 증명의 구조는 비슷하고, 여기서의 matching은 $M' = \{ (i, j) \mid a_i > b_j \}$로 쓰는 것이 자연스럽고, 이 때의 maximum matching을 $M'$이라고 하자. 위의 관찰을 증명하기 위해서는, Dwar에서 Naomi의 득점 최댓값이 $|M'|$이고, 실제로 $|M'|$점을 득점하는 Naomi의 행동이 존재함을 증명하면 된다.

DWar의 최댓값을 먼저 보이자. Dwar의 어떤 라운드의 결과를 $(c, a, b)$라고 쓰자. Naomi가 $c$를 말했고, Ken이 이에 따라 $b$를 제시했으며, Naomi가 최종적으로 $a$를 제시했다는 뜻이다. 결국 득점은 저울로 두 block을 측정한 이후에야 이루어지므로, 위 결과가 점수를 얻은 라운드이려면 $a > b$여야 하므로, DWar에서도 $|M'|$을 넘는 득점은 불가능하다. 따라서 Naomi의 전략이 존재한다는 것만 증명하면 된다. 위와 비슷한 전략이 있다: Ken이 가진 블럭보다 더 큰 값을 부르고, 이 때 Ken이 내게 될 블럭 (보유한 블럭 중 최소 무게)보다 큰 블럭 중 최소인 블럭을 내는 과정을 $|M'|$번 반복한다. 남은 블럭으로는 블러핑 없이 War와 같은 방법으로 대응한다.

핵심은 Ken이 가진 블럭 중 가장 작은 $|M'|$개의 블럭에서 이기는 것이다. 이들을 포함하는 matching이 존재한다는 것은, 아무 maximum matching이나 잡고 거기에 사용된 $b$ 값들 중 가장 작은 $|M'|$개의 블럭이 아닌 것을 바꿔버리는 과정을 반복하면 쉽게 보일 수 있다. $|M'|$점을 획득하고 나면 무슨 전략을 써도 Naomi가 점수를 더 획득할 수 없으니, 문제에서 Ken이 눈치채면 안 된다는 조건을 만족시키기 위해 거짓 정보를 더 이상 부르지 않고 끝내면 된다. 답을 출력하는 건 게임의 실제 진행과 관련이 없고, maximum matching의 값만 구해주면 되는데, 골드 문제이므로 위의 전략을 시뮬레이션하는 게 정해일 것이다. (애초에 matching을 구하는 게 더 복잡하기도 하고)

Ken의 전략이 정말로 유일한지도 의문을 가질 수 있다. 아마 다음의 과정을 거치면 적당히 유의미한 수준의 논의를 전개할 수 있을 것으로 생각한다. 먼저 Ken의 행동을 엄밀하게 정의하자. $f(\{ b_i \}, x, \{ a_i \})$를 Ken의 행동으로 정의하는데, 이는 $\{ b_i \}$가 현재 Ken에게 남은 블럭이며, 여태껏 Naomi가 $\{ a_i \}$를 제시했고, 현재 라운드에서 $x$를 내놓고 그 값을 말해준 상황일 때, Ken이 내게 될 다음 블록을 의미한다. 그러니 $f$는 단순히 말하면 현재까지 Ken이 볼 수 있는 정보 전부를 토대로 열심히 다음 전략을 계산한다는 의미이다. 그러니 context가 충분히 주어져 있으면 이번 라운드의 행동은 적당히 $f(x)$로 표현을 하자. 그러므로 $f$가 Naomi의 전략에 무관하게 (지문에 쓰인 조건 중 하나) Ken이 취할 수 있는 최적의 행동이라는 것은, 초기에 어떤 $\{ a_i \}$와 $\{ b_i \}$가 주어져도, 이들로부터 얻어지는 $a < b$ 꼴의 maximum matching의 크기가 $M$이라고 할 때, Naomi가 어떤 순서로 $x_t$를 제시해도 $M = | \{ (x_t, f(x_t)) \mid x_t < f(x_t) \} |$을 만족해야 함을 의미한다.

위에서 열심히 논의한 바에 따르면, 이전 라운드들의 결과와 Naomi의 행동들은 전혀 고려하지 않아도 무방하다. $x$가 주어지면 $x$ 초과의 최소 블럭을 내놓거나, 없으면 최소 무게 블럭을 내놓는 local한 전략이 최적임을 이미 알기 때문이다. 이제 이것이 유일한 전략임을 증명하기 위해, Ken이 위에서 논의한 최적 전략을 따르지 않으면, 어떤 adversarial한 Naomi에게 주어지는 배열 $\{ a_i \}$가 존재하여, maximum matching을 못 찾는 상황이 나올 수 있음을 보일 것이다. 먼저 특정한 상황에서 $f(x)$가 $f(x) = b_2 > b_1$였다고 하자. $b_1, b_2$는 그 순간 Ken이 가지고 있던 블럭들이고, 특히 $b_1$은 $x$ 초과의 최소 무게 블럭이었다고 하자. 그러면 앞으로 남은 라운드에서 Naomi가 가진 블럭이 전부 $\frac{b_1+b_2}{2}$인 상황에서 maximum matching을 못 찾게 된다. (동일 무게 블럭을 한 사람이 여러 개 가질 수는 없긴 하나, 어차피 블럭 개수가 유한하므로 $\varepsilon$만큼씩 variation을 주면 된다) 또한 Ken이 제시할 블럭이 없는 상황에서 보유하고 있는 블럭 중 최소 무게가 아닌 것을 제시해도 비슷한 현상이 발생한다. 위의 상황에서 $b_1$이 최소 무게이고 $b_2$를 제시했으면, 위와 똑같은 Naomi의 input이 adversarial하다.

$i$행 $j$열이 cow로 채워졌는지 나타내는 boolean 변수를 $c_{ij}$라고 하자. $1$행을 채웠을 때, $c_{1j} = c_{1(j+1)} = 1$인 $j$가 존재하는 경우, 다음이 성립한다: $c_{(2k)j} = c_{(2k)(j+1)} = 0$, $c_{(2k+1)j} = c_{(2k+1)(j+1)} = 1$. 그러므로 $j$열이나 $j+1$열을 관찰하면 cow가 채워졌는지 여부가 alternating함을 확인할 수 있다. 이제 그러한 alternating column에 인접한 $j-1$열을 보자. 이 column은 $c_{1(j-1)}$의 값이 정해지는 순간, 다른 모든 칸이 cow로 채워졌는지 여부가 결정됨을 확인할 수 있다. 또한 둘 중에 어느 경우이든 cow가 채워진 형태가 alternating하다는 성질이 유지됨을 확인할 수 있다. 따라서 이 경우 최종적으로 모든 column이 alternating column이 된다. 게다가 이것이 충분조건이다. 즉 각 열을 그 열의 첫 번째 칸이 채워진 패턴이든 그렇지 않은 패턴이든 아무렇게나 cow로 채운다고 하더라도 문제의 조건을 만족하게 됨을 확인할 수 있다. 맨 앞에서 $c_{1j} = c_{1(j+1)} = 1$이라는 조건이 붙어있긴 하지만, 어쨌든 조건을 만족하는 더 큰 집합을 찾았으니, 추가적으로 분석이 필요한 경우는 항상 $c_{1j} \neq c_{1(j+1)}$인 경우이다.

그러나 이 말은 곧 $1$행이 alternating row라는 의미이고, 위에서 언급한 성질들은 행/열이 다르다고 해서 적용되지 않을 이유가 없으므로, 이제 조건을 만족하는 모든 solution을 서술할 수 있다: 모든 행이 alternating row이거나, 모든 열이 alternating column인 configuration. 따라서 각 행마다 첫 번째 칸이 채워진 경우와 아닌 경우 중 더 높은 value를 가지는 조합을 선택하기만 하면 되고, 열 방향으로도 같은 작업을 해 주면 ok.

이 문제에 왜 그리디 태그가 달려있는지 알 것 같기는 한데, 막상 설명을 하려면 전혀 그리디 같다는 느낌은 안 들고, 오히려 bfs나 dijkstra에 가까운 것 같다. $S_x$를 $x$만큼의 알고리즘 공부량을 가지고 배울 수 있는 알고리즘의 집합이라고 정의하자. 이러면 $S_0 = \emptyset$, $S_{x-1} \subseteq S_x$가 성립한다. 따라서 이론적으로 $S_0, S_1, \cdots$를 전부 구하면, $|S_x| = m$이 되는 최소의 $x$가 곧바로 답이 된다.

어떤 알고리즘 $y$가 $y \not\in S_t$라는 의미는, $S_t$의 모든 알고리즘을 배워도 $y$를 배우는데 필요한 공부량이 $t$보다는 큰 상태라는 것이다. 그러므로 $S_t \nsubseteq S_{t'}$인 최소의 $t'$은 $S_t$에 속한 알고리즘에 의한 공부량 감소를 전부 반영했을 때, 아직 배우지 않은 알고리즘 중 필요한 공부량의 최솟값이 $t'$인 경우가 된다. 따라서 이걸 효율적으로 시뮬레이션하는 방법을 찾으면 그게 곧 풀이이고, dijkstra와 비슷하게 접근해서 priority queue를 사용하거나, 골드이긴 하지만 segment tree를 사용하면 되겠다.