Non-Recursive Implementation of FFT

Mon May 24 2021

Discrete Fourier Transform(DFT)

DFT란 주어진 다항식 $\,f(x)=\sum a_i x^i$의 coefficient representation에서 point-value representation으로의 변환을 의미한다. 또한 IDFT(Inverse DFT)는 그 역과정을 의미한다. 이론적 배경에 대한 설명은 본 글의 주목적은 아니니, 내가 공부한 참고문헌에 써놓았다.

Fast Fourier Transform(FFT)

DFT, IDFT를 효율적으로 계산하고 처리하는 과정을 FFT이라고 부른다. 일반적인 $n$차 다항식에서는 각각의 point-value를 계산하는데 $O(n)$ 시간이 걸리므로 전체 시간복잡도는 $O(n^2)$이나, DFT와 IDFT 모두 $O(nlogn)$에 처리하는 방법이 있다. 이들 중 가장 대표적인 방법이 Cooley-Tukey algorithm으로, Divide and Conquer 방법론을 따르는 간단한 알고리즘이다.

Recursive Implementation

Cooley-Tukey algorithm은 $n=ab$로 분할될 때 크기가 $a$, $b$인 작은 문제를 풀어 이를 합친다. 보통은 $n=2^k$로 차수를 확장하여 정확히 절반을 쪼개는 방법을 많이 사용한다. 재귀, 비재귀적 구현 모두 Divide와 Conquer 과정에서 다항식의 크기가 짝수임을 활용하는 부분이 군데군데 있다. 또한 모든 Divide 과정에서 크기가 짝수라는 성질이 만족되려면, $n$은 2의 거듭제곱꼴만 가능하다. 따라서 분석할 다항식의 차수가 2의 거듭제곱꼴이 아니라면, 차수를 늘리고 고차항의 계수는 0인 것으로 보면 된다.

실제 logic은, even 함수와 odd 함수 두 개에 대해 재귀를 돌려 얻은 point-value값을 전체 다항식의 point-value값으로 합치면 된다. 그러나 재귀는 일반적으로 성능면에서 좋지 못하다. 함수의 return이 $O(n)$번 일어날 뿐더러, FFT의 경우 공간복잡도가 $O(nlogn)$에 달하기 때문이다. 따라서 여기에서는 iterative version의 FFT 구현을 살펴보겠다.

Non-Recursive Implementation

대략의 mental model은, 길이 $n$ 정도의 배열에서 값의 update를 적당한 위치에서 반복하는 것이다.
전체 다항식의 길이 $n$에 대한 root of unity $\omega$에 대해, $\,f(\omega^{k}), \,f(\omega^{k+\frac{n}{2}})$의 값을 계산하는데는 $\,f_{even}(\omega^{2k}), \,f_{odd}(\omega^{2k})$의 값만 필요하다. 따라서 $\,f_{even}$과 $\,f_{odd}$의 FFT 결과값이 배열 상에서 인접한 위치에 쓰여있었다면 $\frac{n}{2}$칸씩 떨어진 값을 pair로 보고 값을 갱신한다. 이렇게 되면 Divide의 결과값의 위치와 Conquer 이후 결과값이 위치해야 할 곳이 정확히 맞물림을 알 수 있다. 자세히 말하면 Conquer 이후의 결과는 Divide의 결과값으로 가정했던 point-value가 연속한 위치에 있어야 한다는 조건을 만족한다는 의미이다.

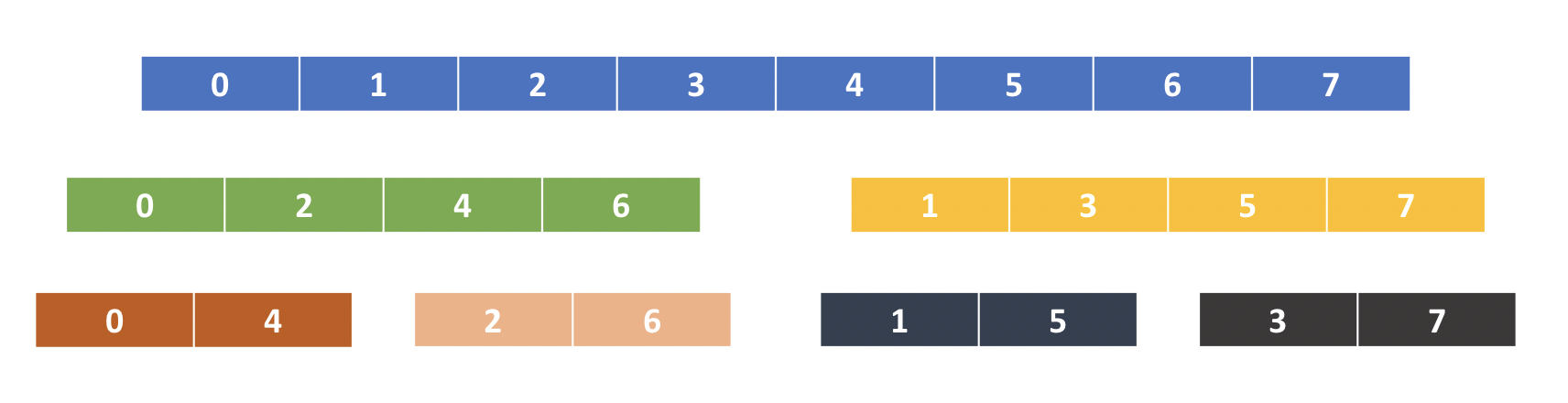
이렇게 되면 초기화를 해야한다. 길이가 1일 때는 coefficient의 값이 곧 바로 point-value와 같으나, 그림의 가장 하단을 보면 coefficient의 순서가 전체적으로는 0, 1, 2, ... 순으로 위치하지 않았다. 따라서 저 순열을 어떻게 만들 수 있는지 확인해야 하는데, 각각의 값을 bit로 표현하고 이를 뒤집어보자. 신기하게도 그 값이 0부터 1씩 증가하는 형태이다.

직관적인 설명은 다음과 같다. 최종 상태에서 거꾸로 초기 상태로 가는 과정을 생각해보면, least significant bit(LSB)가 짝수인 것이 왼쪽, 홀수인 것이 오른쪽으로 가는 형태이므로 bit를 뒤집은 입장에서는 most significant bit(MSB)가 1인 것이 오른쪽으로 몰리는 형태이기 때문이다. 모든 끝자리 bit에 대해 이 과정이 반복되므로, bit를 뒤집은 값은 오른쪽으로 갈수록 커질 수밖에 없다.

코드에서 FFT() 함수 내의 첫 번째 부분이 초기화 부분인데, 이는 덧셈의 자리올림 과정을 최상위 bit를 LSB에 적용하기 시작하는 과정으로 볼 수 있다. 약간만 생각해보면 무슨 말인지 알 수 있을 것이다. 그러므로 32bit 정수 전체를 뒤집고 $n$에 대한 상수값만큼 shift시키는 방법으로 이 과정을 약간 더 최적화할 수 있겠다. 다만 병목 지점은 Divide and Conquer 부분이므로, 큰 의미는 없겠다.

Multiplication of Polynomials

FFT를 이용해 point-value representation을 빠르게 구하고 그 역변환이 가능하다는 점을 이용하면, 차수가 $n$인 두 다항식의 곱셈도 대략 $O(nlogn)$에 가능하다. 두 다항식의 point-value를 구하고 각각을 곱하면 두 다항식의 곱에 대한 point-value가 만들어진 셈이며, 이를 IDFT 취하면 곱셈 결과가 coefficient representation로 얻어지기 때문이다.

따라서 DFT 2번 -> point-value multiplication -> IDFT 1번을 거치면 다항식의 곱셈이 가능한데, 여기서 시간을 빠르게 하기 위한 한 가지 trick이 더 존재한다. 실계수 다항식 $f(x)$와 $g(x)$를 point-value로 만드는 과정을 새로운 다항식 $P(x)=f(x)+ig(x)$의 DFT 1번으로 대체할 수 있다. $n$이 짝수이므로 $\overline{\omega^{k}} = \omega^{n-k}$가 성립하는데, 이로부터 아래의 식을 유도할 수 있다.

$$ f(\omega^{k}) = \cfrac{P(\omega^{k}) + \overline{P(\omega^{n-k})}}{2},\,\, g(\omega^{k}) = \cfrac{P(\omega^{k}) - \overline{P(\omega^{n-k})}}{2i} $$

즉 $O(n)$의 추가 연산만으로 DFT 2번을 한 효과가 생긴다.

Code

typedef complex<double> base;
const double PI = acos(-1);

void fft(vector<base>& a, bool inv) {
    int n = a.size();
    for (int dest=1, src=0; dest<n; ++dest) {
        int bit = n / 2;
        while (src >= bit) {
            src -= bit;
            bit /= 2;
        }
        src += bit;
        if (dest < src) { swap(a[dest], a[src]); }
    }

    for (int len=2; len <= n; len *= 2) {
        double ang = 2 * PI / len * (inv ? -1 : 1);
        base unity(cos(ang), sin(ang));
        for (int i=0; i<n; i+=len) {
            base w(1, 0);
            for (int j=0; j<len/2; ++j) {
                base u = a[i+j], v = a[i+j+len/2] * w;
                a[i+j] = u+v;
                a[i+j+len/2] = u-v;
                w *= unity;
            }
        }
    }

    if (inv) {
        for (int i=0; i<n; ++i) { a[i] /= n; }
    }
}

void multiply(const vector<int>& a, const vector<int>& b, vector<int>& result) {
    int n = 2;
    while (n < a.size() + b.size()) { n *= 2; }

    vector<base> p(a.begin(), a.end());
    p.resize(n);
    for (int i=0; i<b.size(); ++i) { p[i] += base(0, b[i]); }
    fft(p, false);

    result.resize(n);
    for (int i=0; i<=n/2; ++i) {
        base u = p[i], v = p[(n-i) % n];
        p[i] = (u * u - conj(v) * conj(v)) * base(0, -0.25);
        p[(n-i) % n] = (v * v - conj(u) * conj(u)) * base(0, -0.25);
    }
    fft(p, true);
    for (int i=0; i<n; ++i) { result[i] = (int)round(p[i].real()); }
}